まずは、登場する文字の確認をしよう

\(m\):質量
\(a\):加速度
\(F\):力

物体にある一定の力\(F\)を加えて、
加速度\(a\)を生むことを考えると、

物体の質量\(m\)が大きいほど、加速度\(a\)は小さく、
物体の質量\(m\)が小さいほど、加速度\(a\)は大きくなる

ざっくりいうと、

質量\(m\)が大きいほど、動きにくい、
質量\(m\)が小さいほど、よく動く。

この内容をうまくいうと、

質量\(ｍ\)は、物体の動きにくさ

といえる。

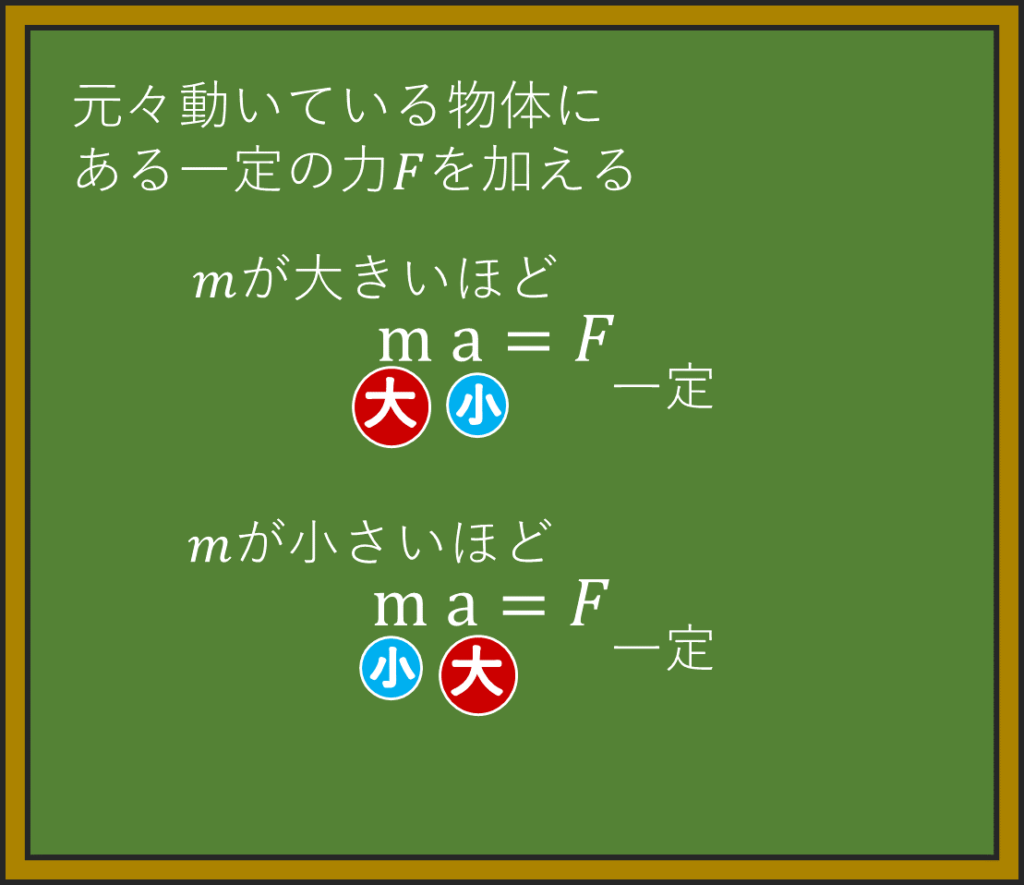
今度は、元々動いてる物体に、
逆向きの力を\(F\)（ブレーキ）を加えて
逆向きの加速度\(a\)（減速）を生むことを考えよう。

この場合でも、さっきと同様に

物体の質量\(m\)が大きいほど、加速度\(a\)は小さく、
物体の質量\(m\)が小さいほど、加速度\(a\)は大きくなる

ざっくりいうと、

質量\(m\)が大きいほど、減速しづらい、
質量\(m\)が小さいほど、すぐ止まる。

この内容をうまくいうと、

質量\(m\)は、動いてる物体の止めにくさ

ともいえる。

これらをまとめて、

質量\(m\)は、物体の動きにくさ/動いてる物体の止めにくさ

を表すものといえる。

おまけ

\(F=kx\)からばね定数\(k\)の意味を考えよう。

まずは、登場する文字の確認をしよう

\(F\):力
\(k\):ばね定数
\(x\):変位（ばねの伸び）

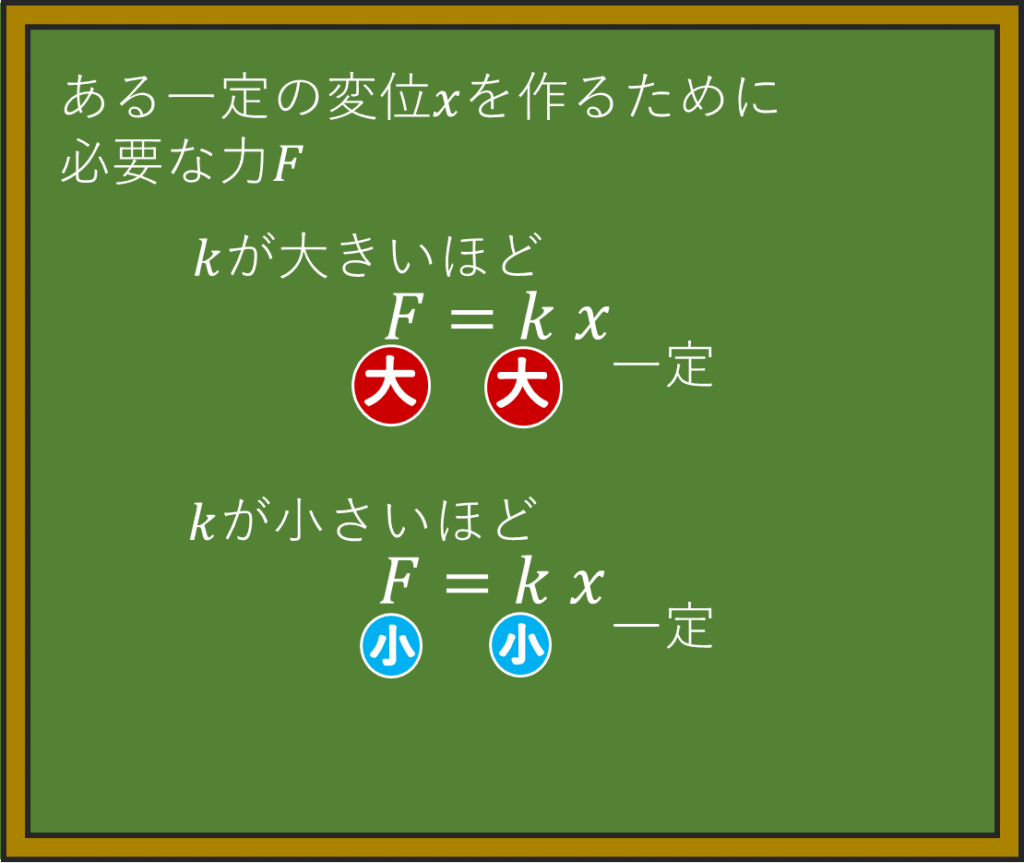
物体にある一定の変位\(x\)（伸び\(x\)）を作るために、
必要な力\(F\)を考えると、

物体のばね定数\(k\)が大きいほど、必要な力\(F\)は大きく、
物体のばね定数\(k\)が小さいほど、必要な力\(F\)は小さくなる

ざっくりいうと、

ばね定数\(k\)が大きいほど、硬い、
ばね定数\(k\)が小さいほど、柔らかい。

この内容をうまくいうと、

ばね定数\(k\)は、ばねの硬さ

といえる。

最後に

相模大野個別指導塾には、東大や東工大出身の数学が大好きな講師がたくさんいるため
他にも高校物理でわからない問題があった時、すぐにその疑問を解決できます！
一緒に苦手を克服し、志望校合格を掴みましょう！！