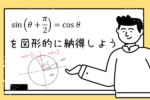
まず、単位円(半径1の円)を考えます。
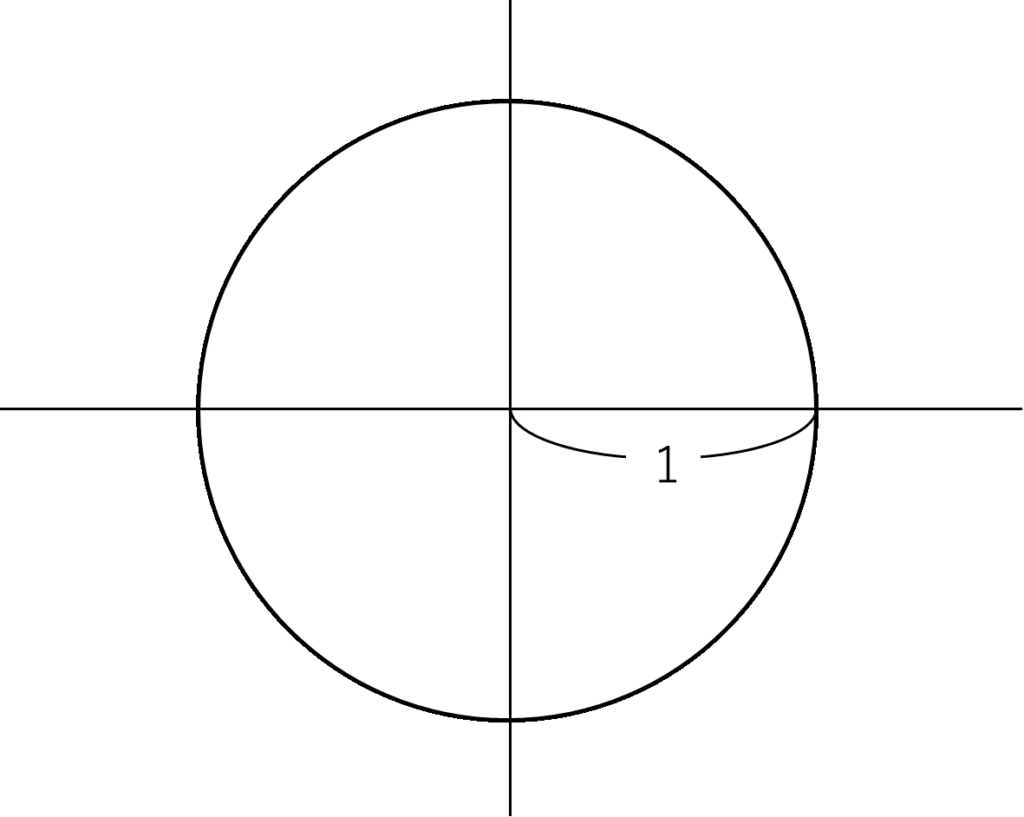
図のように\(\theta\)をとる。
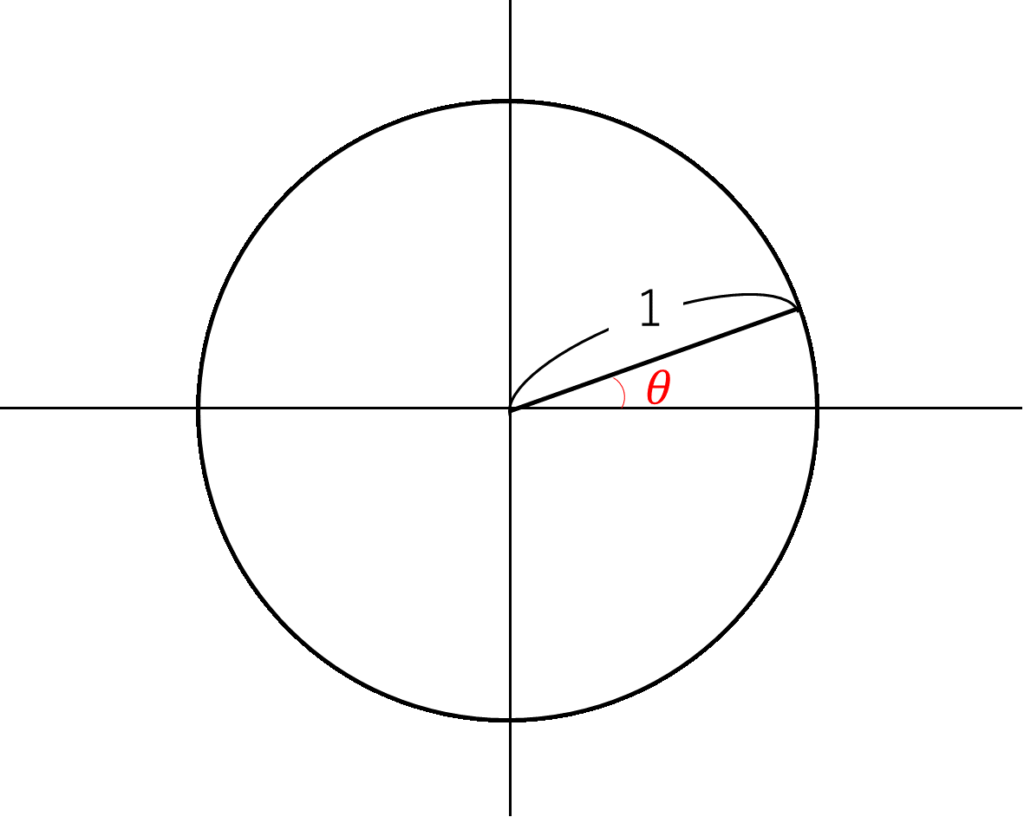
\(\sin\theta\),\(\cos\theta\)は以下の部分になります。
\(\theta+\frac{\pi}{2}(\theta+90^\circ)\)を考えると
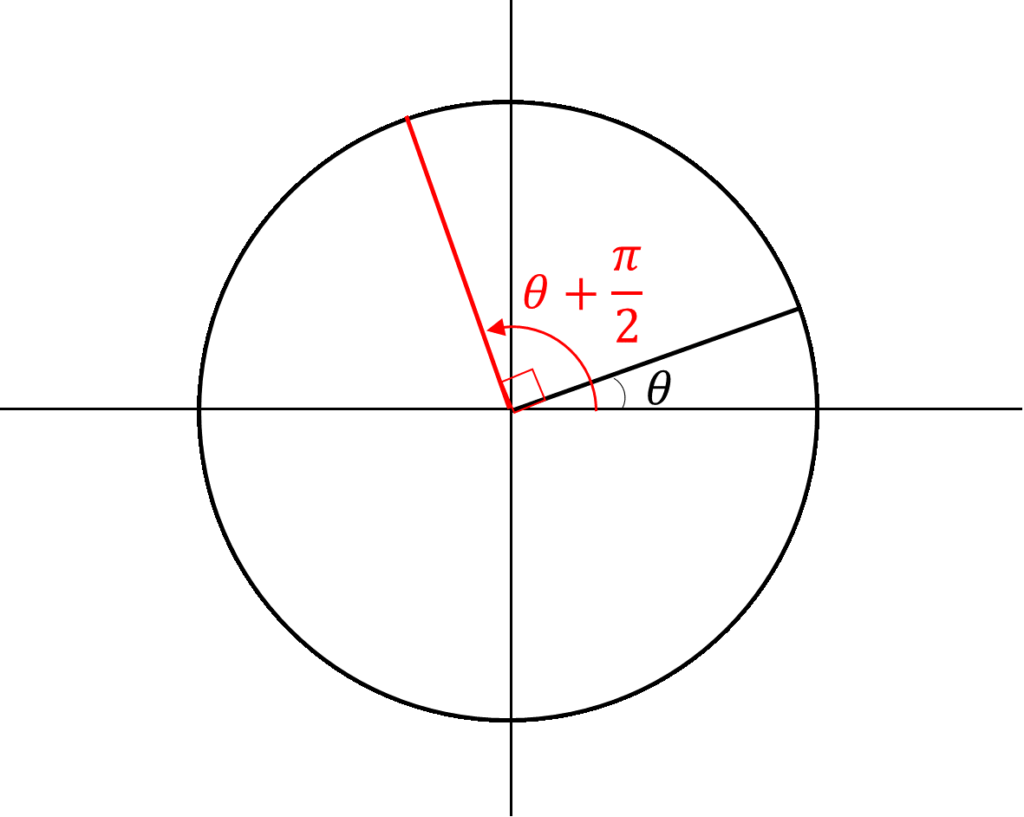
もう少し情報を書いて、
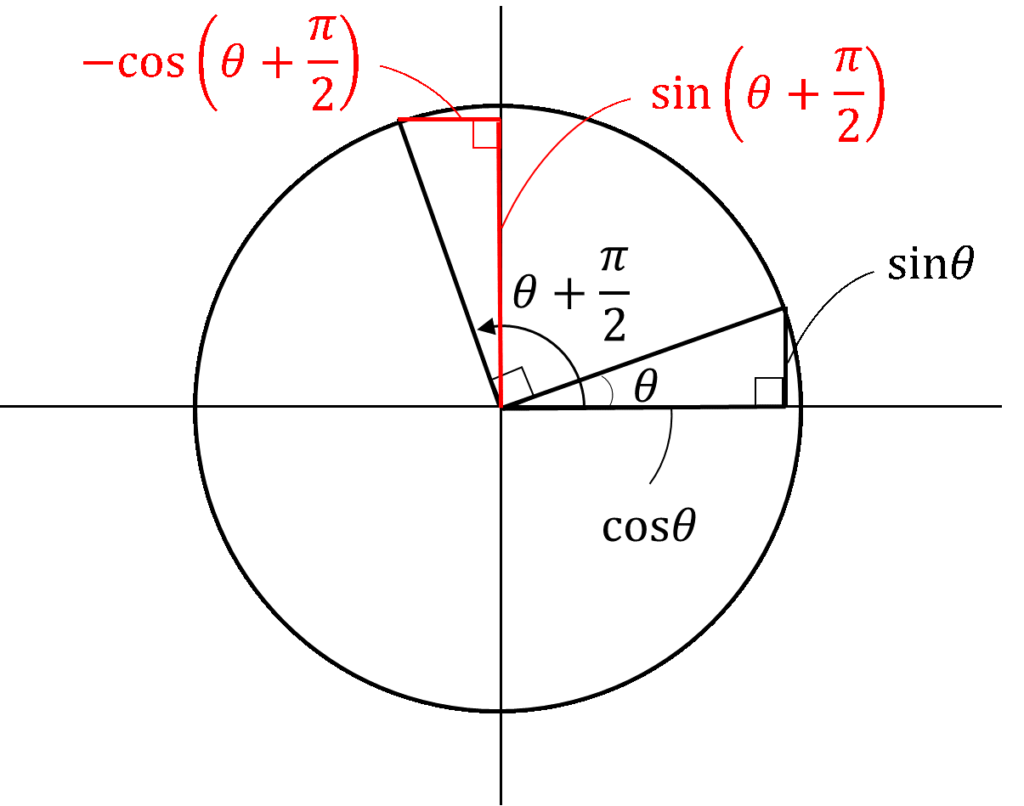
( この図だと\(\cos(\theta+\frac{\pi}{2})\)は負の値なので、
\(-\cos(\theta+\frac{\pi}{2})\)として正にしています。 )
以下の図形に注目します。
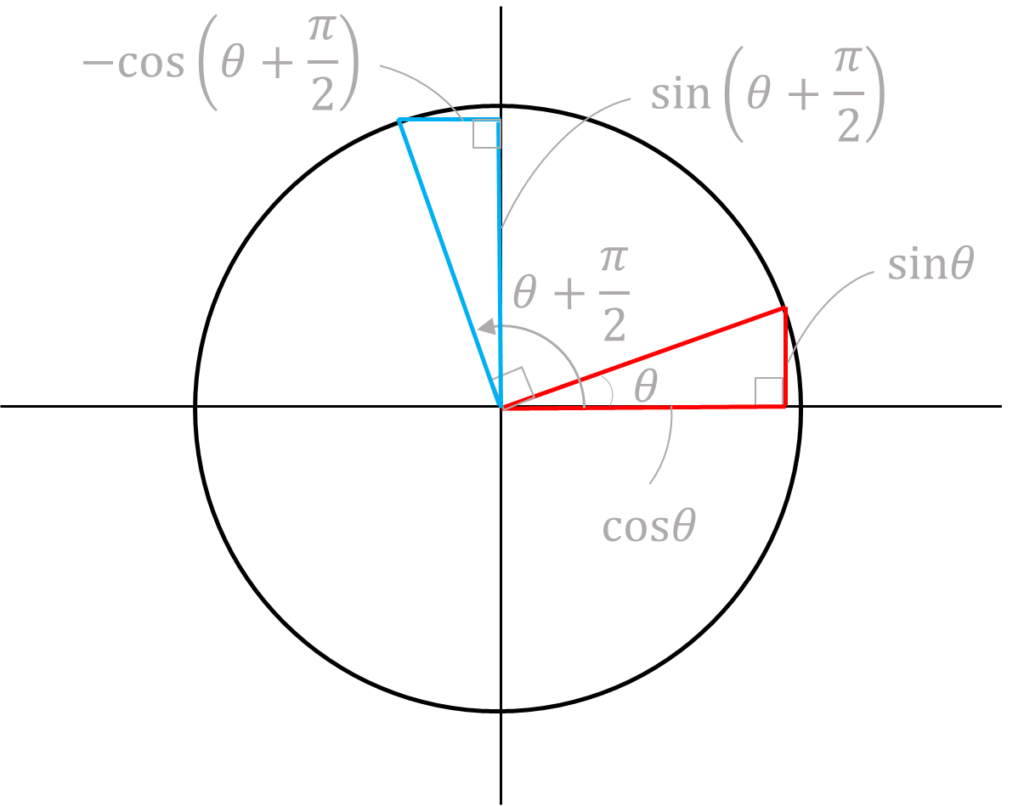
青の三角形と赤の三角形は
合同になっています。(ぴったり重なる)
合同なので、対応する辺は等しく
\(\sin(\theta+\frac{\pi}{2})=\cos\theta\)
です。
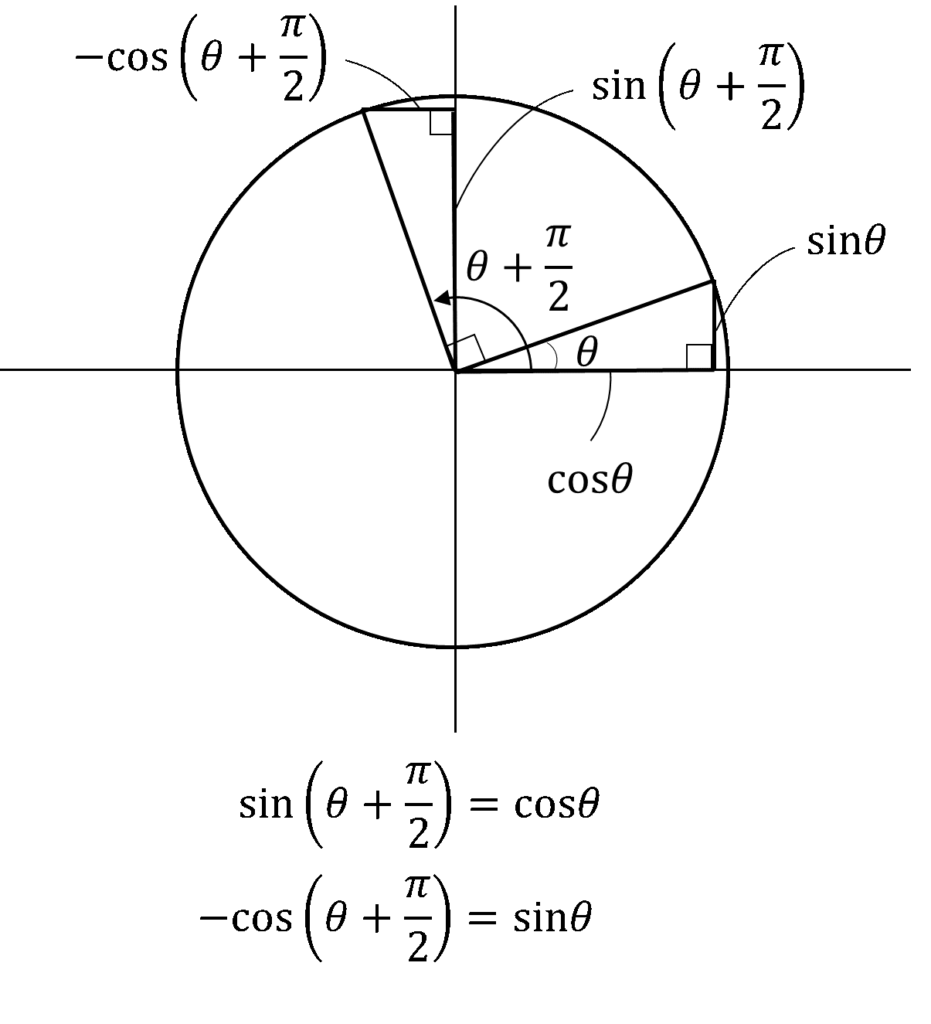
最後に
相模大野個別指導塾には、東大や東工大出身の数学が大好きな講師がたくさんいるため
他にも高校数学でわからない問題があった時、すぐにその疑問を解決できます!
一緒に苦手を克服し、志望校合格を掴みましょう!!
志望校合格への3つの秘訣!!
①生徒様にあった学習プランを提供
②一人一人に寄り添った丁寧な指導
③「話す授業」で理解度をアップ
より詳しいことは下のボタンをクリックしてください