突然ですが、次の問題はどう解くだろうか

途中\(x^2+3x+2=0\)を解く場面がありました。
つまり

と考えても良いだろう

図で示すと

これをふまえて、次の問題を考えてみよう。

\(x^2+3x+2=k\)の解は
2つのグラフ
\(\begin{eqnarray} \left\{ \begin{array}{l} y = x^2+3x+2 \\ y = k \end{array} \right. \end{eqnarray}\)
の交点の\(x\)座標と考えます。
\(\begin{eqnarray} y&=&x^2+3x+2 \\ y&=&(x+\frac{ 3 }{ 2 })^2-\frac{ 1 }{ 4 } \end{eqnarray}\)
ですから、2つのグラフは以下のようになります。

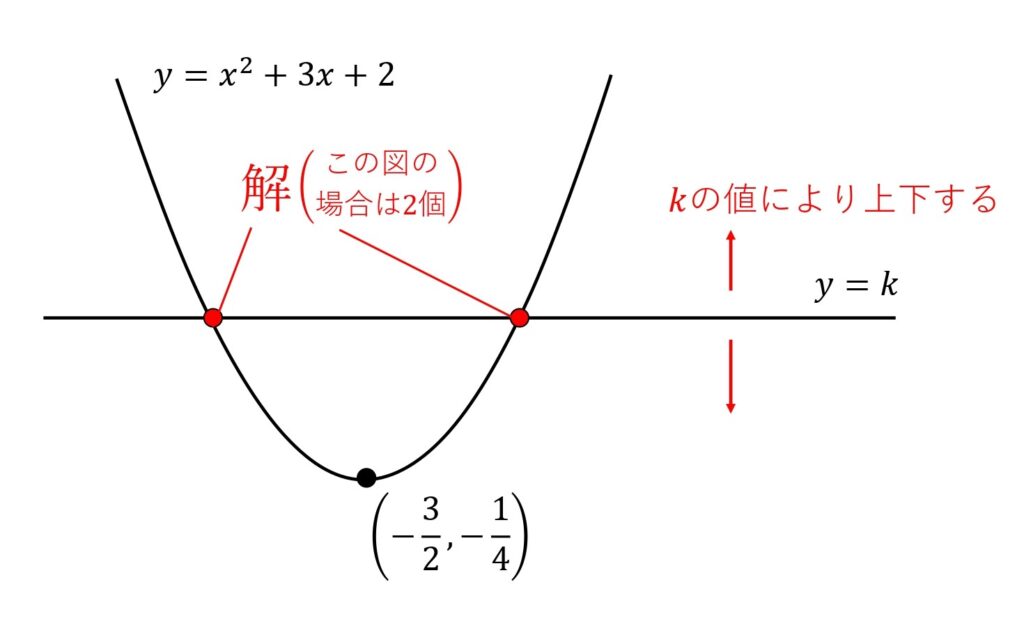
\(k\)の値と解の個数は

i)　\(k\gt-\frac{1}{4}\) のとき

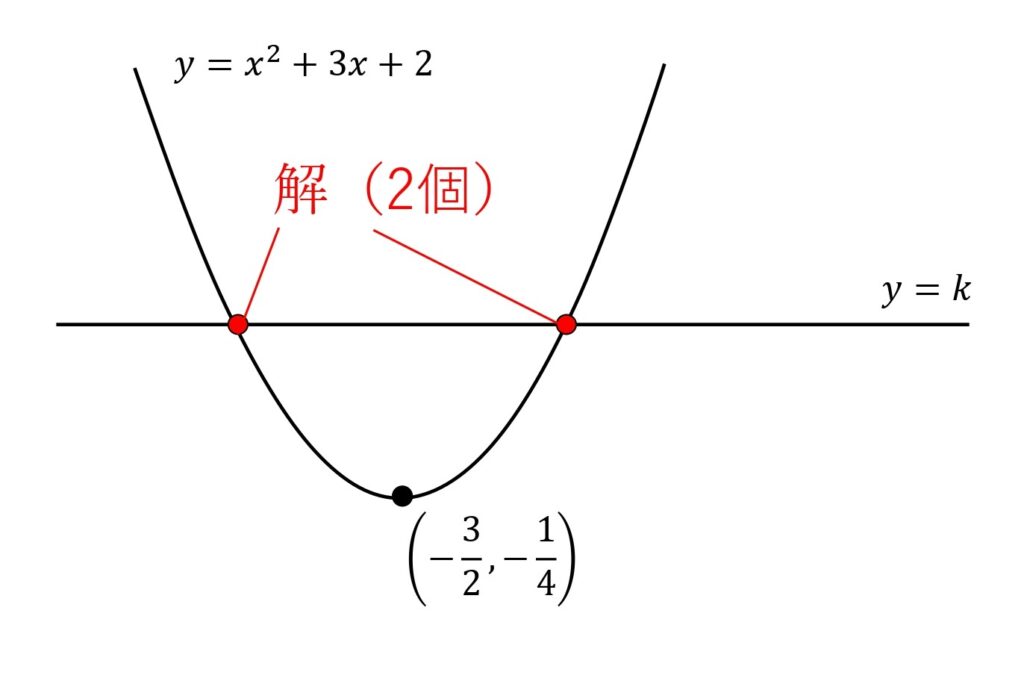
解は2個

ii)　\(k=-\frac{1}{4}\)のとき

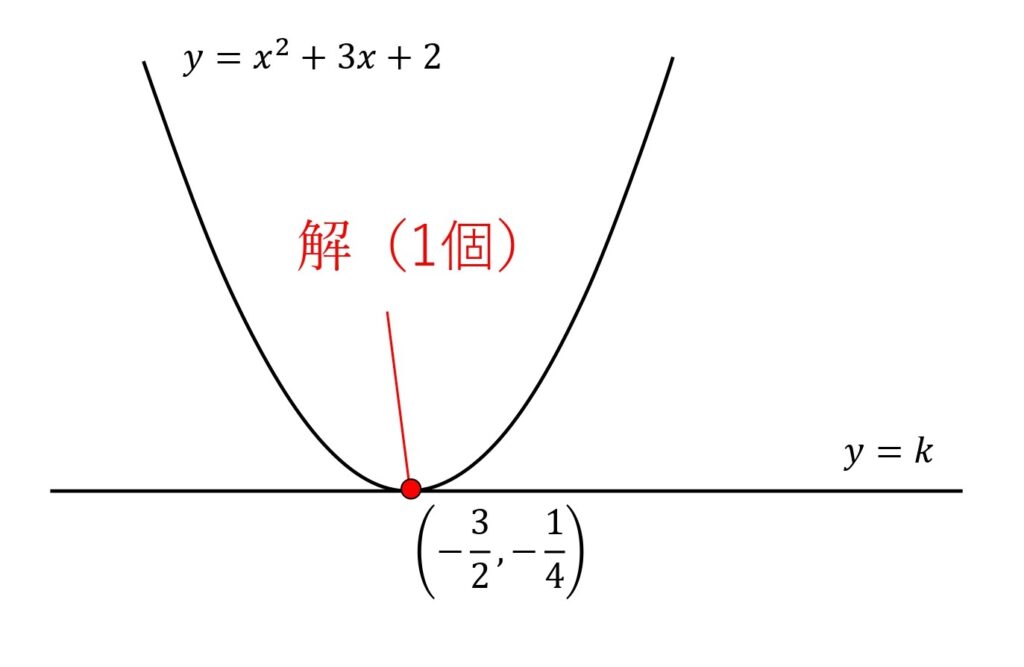
解は1個

iii)　\(k\lt-\frac{1}{4}\)のとき

解は0個

まとめると

答え
\(k\gt-\frac{1}{4}\) のとき、解は2個、
\(k=-\frac{1}{4}\)のとき、解は1個、
\(k\lt-\frac{1}{4}\)のとき、解は0個

図形的な視点、イメージがあると応用的な問題に立ち向かいやすくなります。
単純な式が意味あるものに見えて面白いということもあると思います。
今回の内容が勉強の励みになっていたらうれしいです。