学校の物理に苦手意識を持っていませんか、なんとなく図を書いて場当たり的に解いていないだろうか、高校物理の力学は、解く手順が明確になっていれば難しい問題にも立ち向かえるようになります。
易しい問題と難しい問題の2問を通しながら確認していこう。
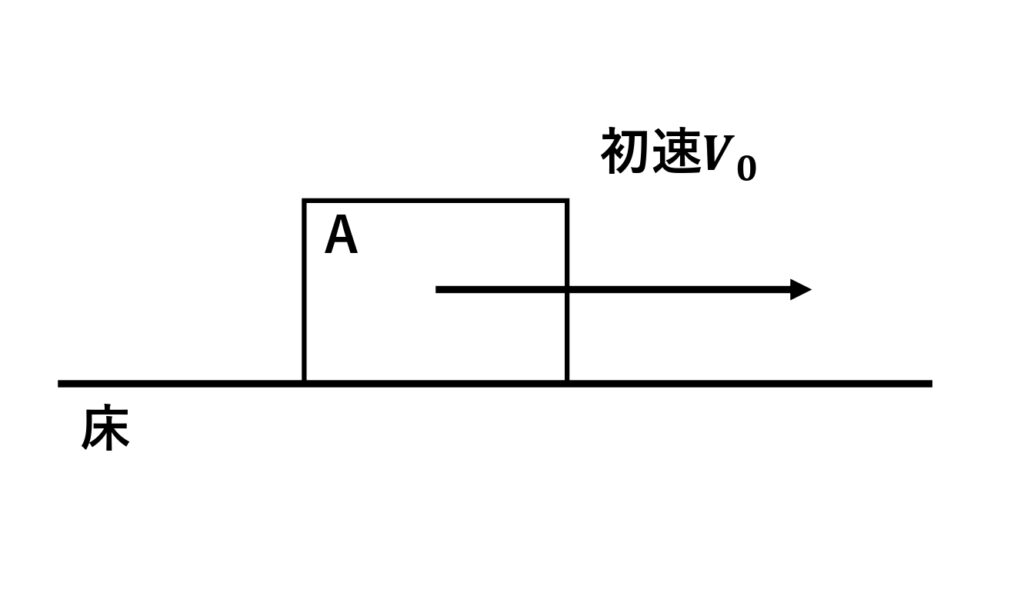
図のように質量\(\normalsize{m}\)の物体\(\normalsize{A}\)が床の上を初速\(\normalsize{V}_{0 }\)で動いている。
物体\(\normalsize{A}\)と床都の間に摩擦\(\normalsize{g}\)あるとき、物体\(\normalsize{A}\)が静止するまでにかかる時間はいくらか。
ただし物体\(\normalsize{A}\)と床との動摩擦係数は\(\normalsize{\mu}\)とする。
1 力の図示
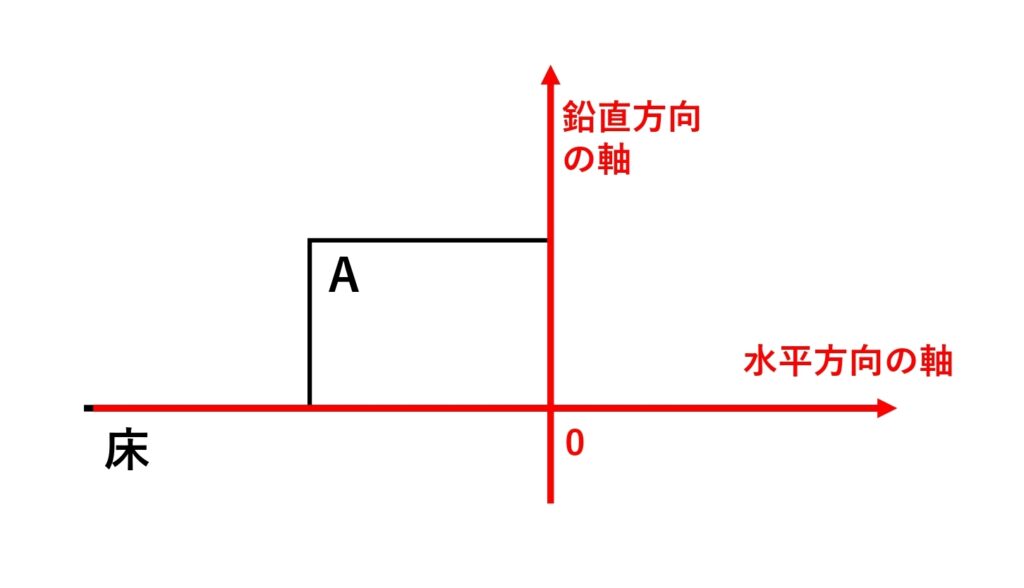
1-1 注目物体と軸を決める
物体Aで軸は図のように設定します。
1-2 重力を書く
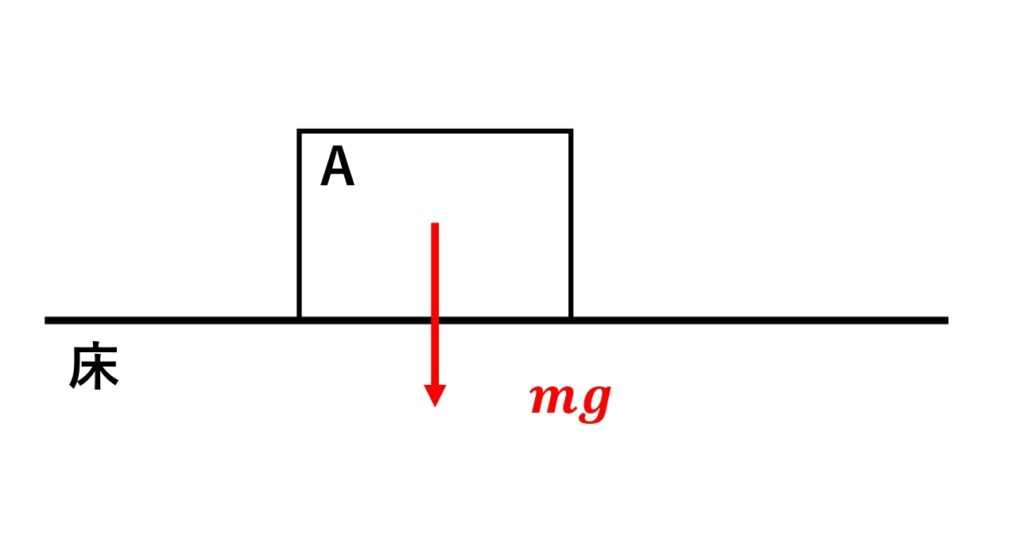
1-3 直接触れているところから受ける力 を書く
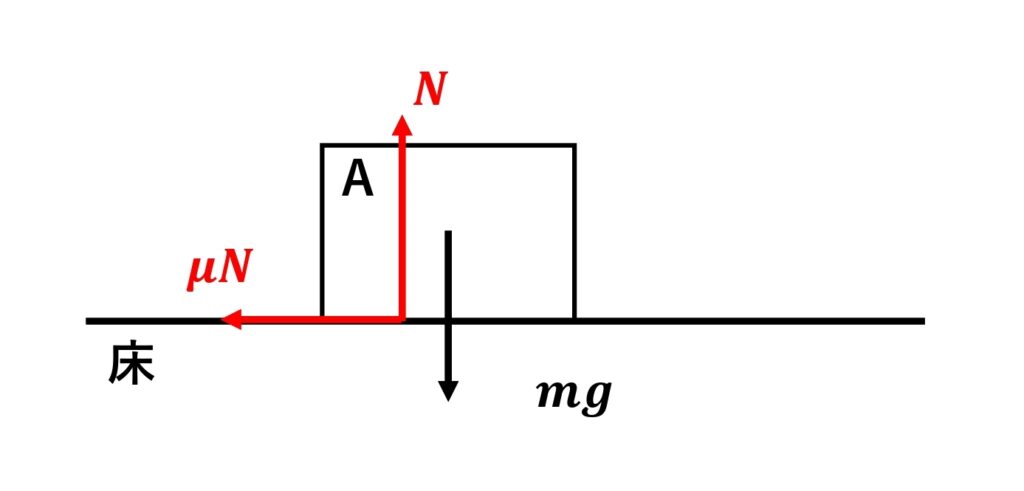
※摩擦力は\(\normalsize{\mu}\normalsize{N}\)
(摩擦係数)×(垂直抗力)
です。
2 式を立てる
書いた図を見ながら式を立てる
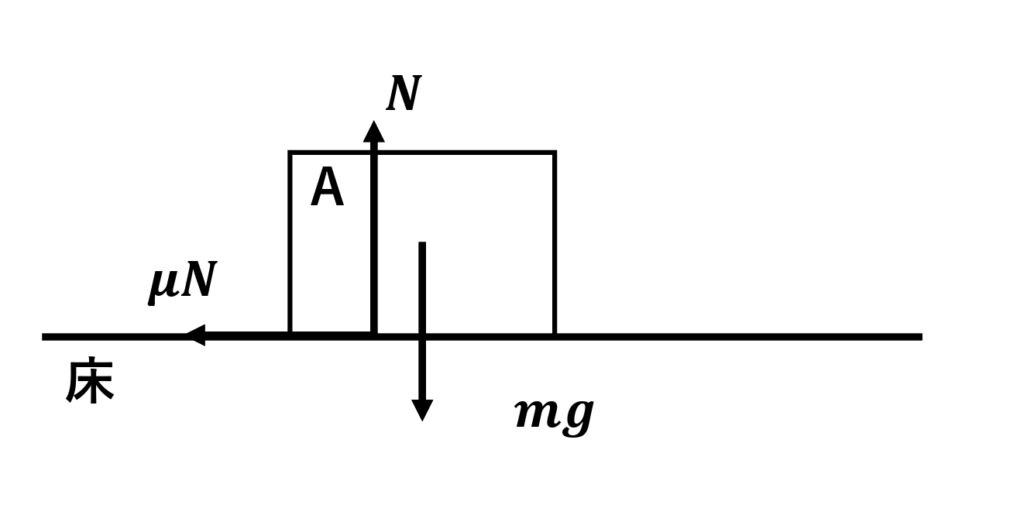
鉛直方向(上下方向)
\(\normalsize{N}=\normalsize{mg}\) (つりあっているのでつりあいの式)
水平方向(左右方向)、物体Aの加速度を、右向きを正として
\(\normalsize{ma}=-\normalsize{\mu}\normalsize{N}\) (つりあっていないので\(\normalsize{ma}=\normalsize{F}\))
↑マイナスがつくのは\(\normalsize{\mu}\normalsize{N}\)が左向きの力だから
3 式をいじって答えを出す。
立てた式をいじっていきます。
\begin{eqnarray} \left\{ \begin{array}{l} \normalsize{N}=\normalsize{mg} \\ \normalsize{ma}=-\normalsize{\mu}\normalsize{N} \end{array} \right. \end{eqnarray}
\(\normalsize{N}\)を消去し
\(\normalsize{a}=-\normalsize{\mu}\normalsize{g}\)
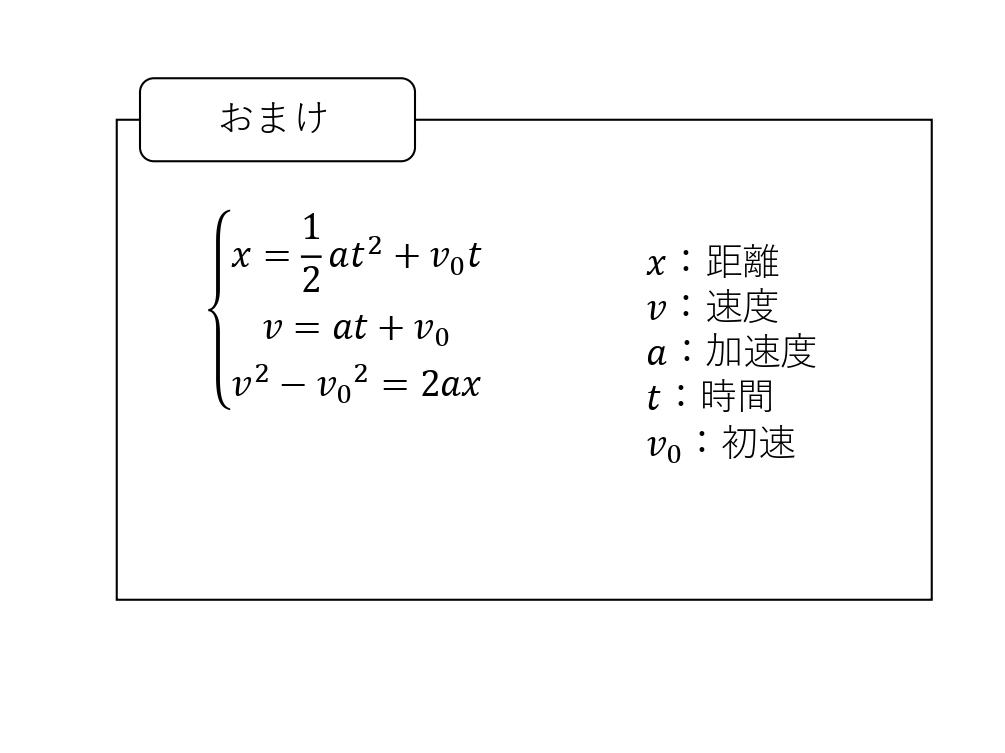
\(\normalsize{V}=\normalsize{at}+\normalsize{V}_{0 }\) より[おまけを確認] \(\normalsize{V}=\normalsize{0}\)となるのは
\begin{eqnarray} \normalsize{V}=\normalsize{at}+\normalsize{V}_{0 }\\ \normalsize{V}=-\normalsize{\mu}\normalsize{gt}+\normalsize{V}_{0 }\\ \normalsize{t} = \frac{ \normalsize{V}_{0 }}{\normalsize{\mu}\normalsize{g}} \end{eqnarray}
(答え \(\frac{ \normalsize{V}_{0 } }{ \normalsize{\mu}\normalsize{g} }\))
図のように床の上に物体B、物体Bの上に物体Aが置かれ、物体Aに初速\(\normalsize{v}_{0}\)が与えられた。
床と物体Bとの間には摩擦はなく、物体Bと物体Aの間には摩擦があるとき、少しして物体Aは物体Bの上で止まった。
止まるまでにかかった時間はいくらか
ただし、物体Bと物体Aとの動摩擦係数をμとし、物体Bの質量をM、
物体Aの質量をm、初め物体Bは静止しているとする。
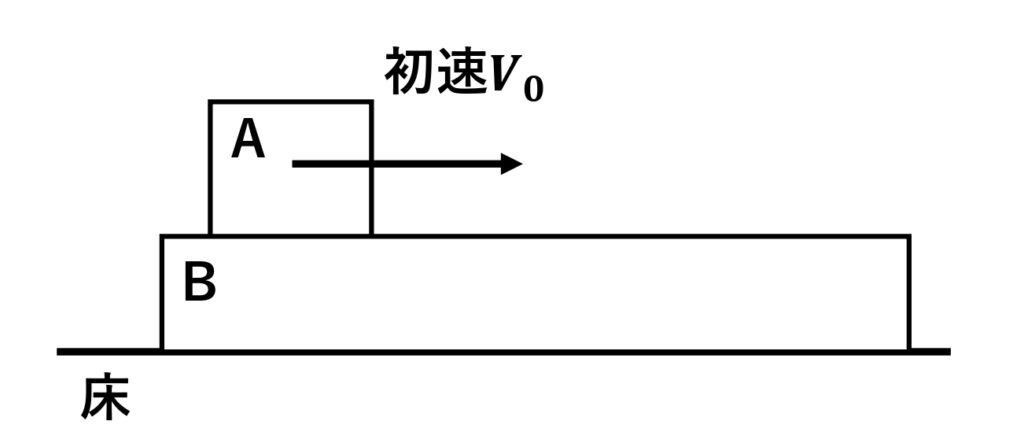

☆注目物体を明確にしておくと混乱しにくい
[A]
1 力の図示
1-1 注目物体と軸を決める
まずは、物体Aに注目します。
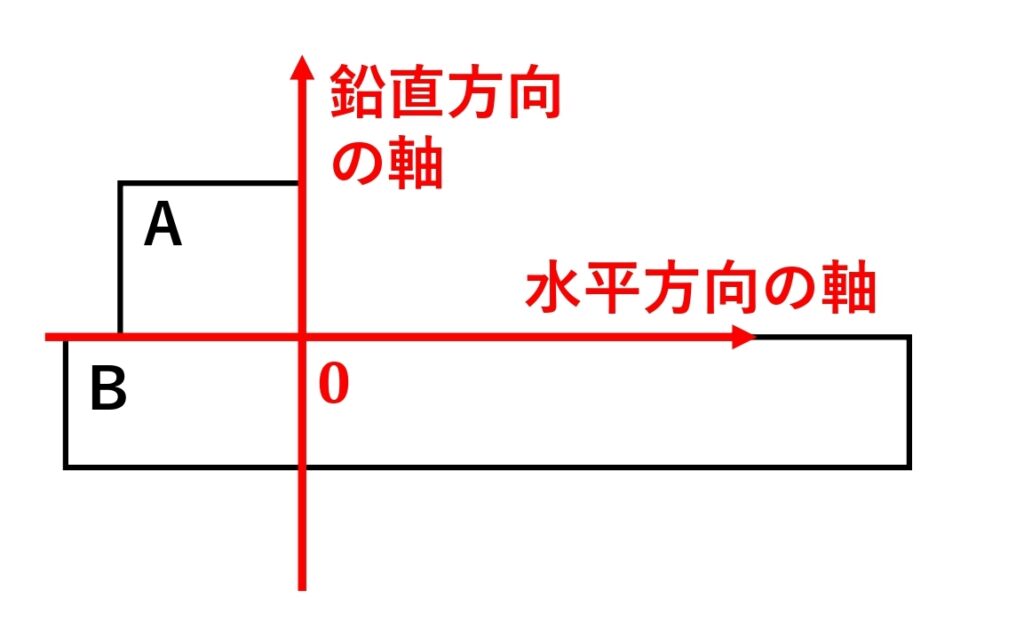
1-2 重力を書く
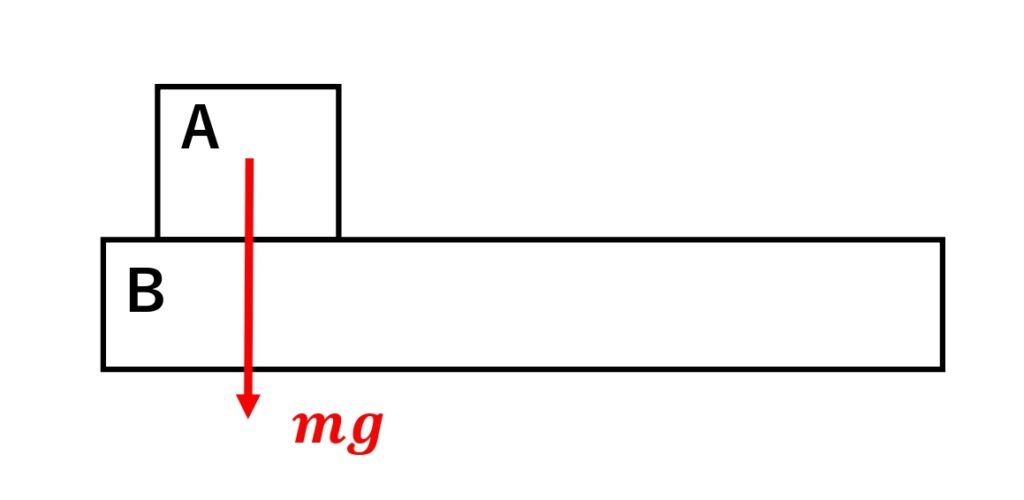
1-3 直接触れているところから受ける力を書く。
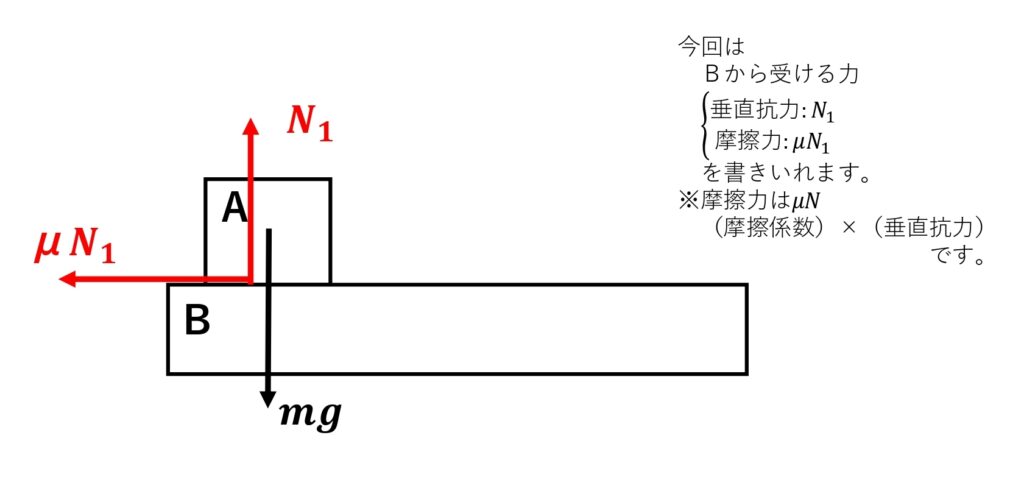
2 式を立てる
書いた図を見ながら式を立てる
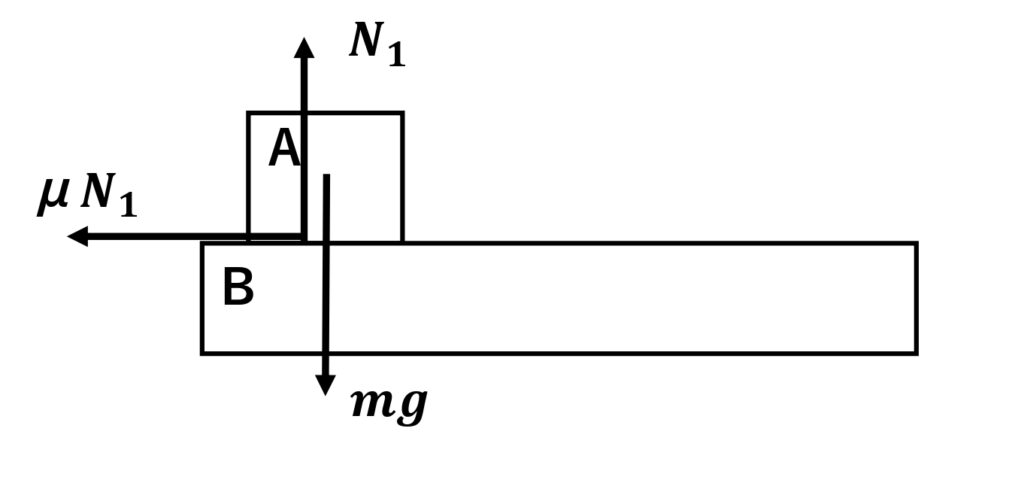
鉛直方向(上下方向)
\(\normalsize{ N }_{ 1 }=\normalsize{ mg }\)(つりあっているのでつりあいの式)
水平方向(左右方向)、物体\(\normalsize{ A }\)の加速度を\(\normalsize{ a }\)、右向きを正として
\(\normalsize{ ma }=-\normalsize{ \mu }\normalsize{ N }_{1}\)(つりあっていないので\(\normalsize{ ma }=\normalsize{ F }\))
↑マイナスがつくのは\(\normalsize{ \mu }\normalsize{ N }_{1}\)が左向きの力だから
これ以上は話が進まないので、次に\(\normalsize{ B }\)に注目していきます。
\(\normalsize{ B }\)
1 力の図示
1-1 注目物体と軸を決める
次に、物体\(\normalsize{ B }\)に注目します。
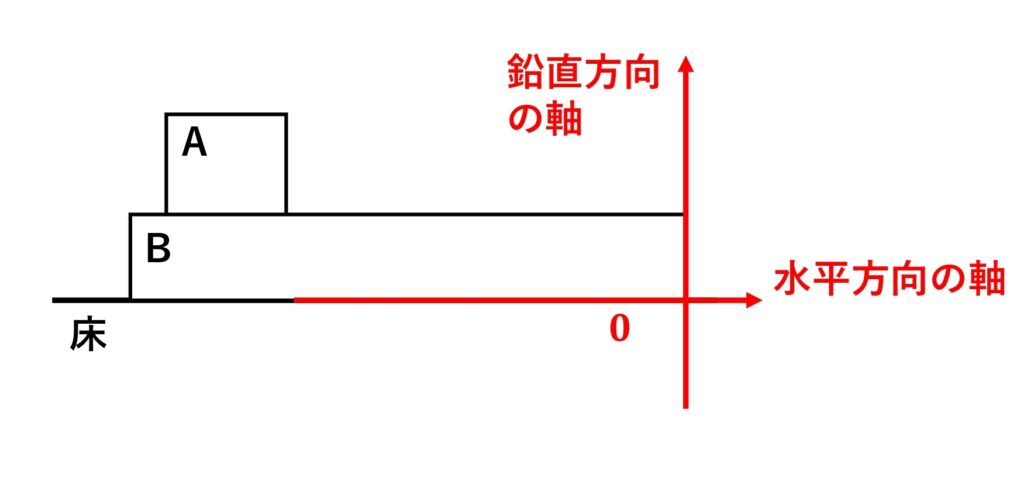
1-2 重力を書く
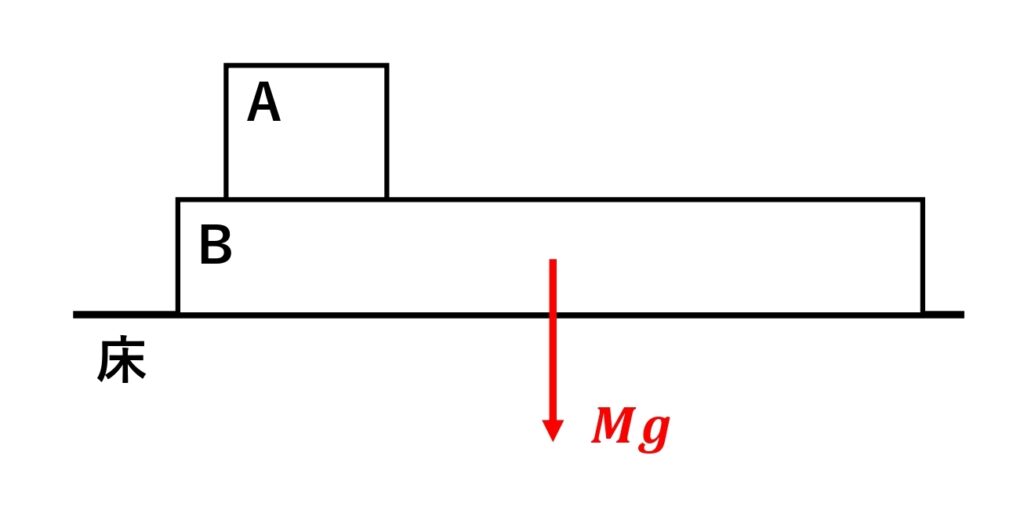
※\(\normalsize{ B }\)に注目しているので\(\normalsize{ B }\)の重力\(\normalsize{ mg }\)は書かない
1-3 直接触れているところから受ける力を書く
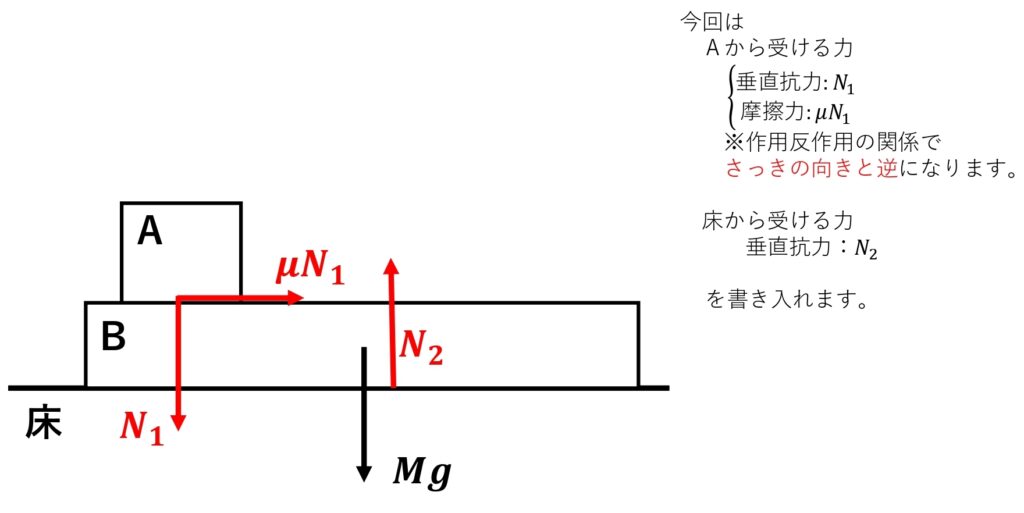
2 式を立てる
書いた図を見ながら式を立てる
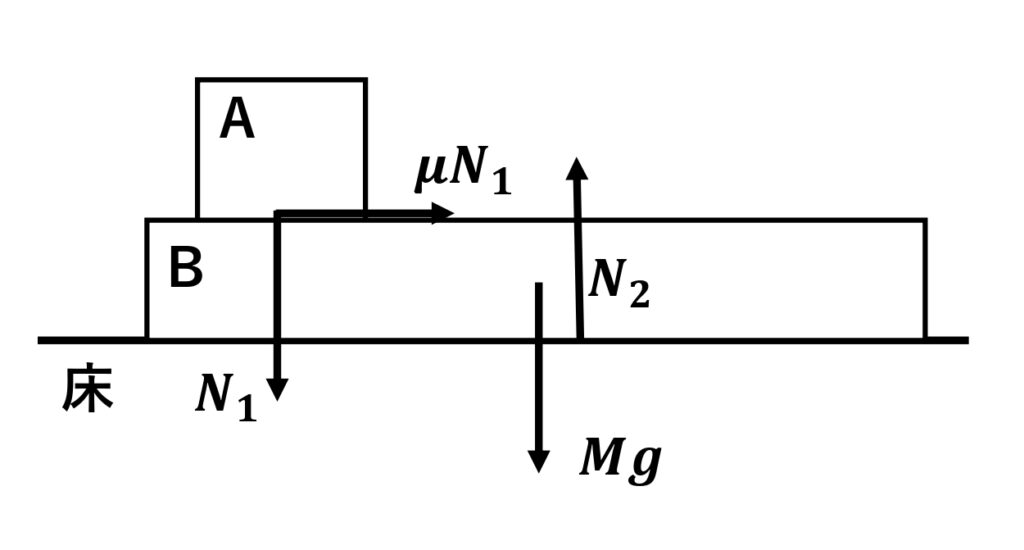
鉛直方向(上下方向)
\(\normalsize{ N }_{ 2 }=\normalsize{ N }_{1}+\normalsize{Mg}\)(つりあっているのでつりあいの式)
水平方向(左右方向)、物体\(\normalsize{B}\)の加速度を\(\normalsize{A}\)、右向きを正として
\(\normalsize{MA}=\normalsize{\mu}\normalsize{N}_{1}\)(つりあっていないので\(\normalsize{ma}=\normalsize{F}\))
3 AとBの最後の式をいじっていく
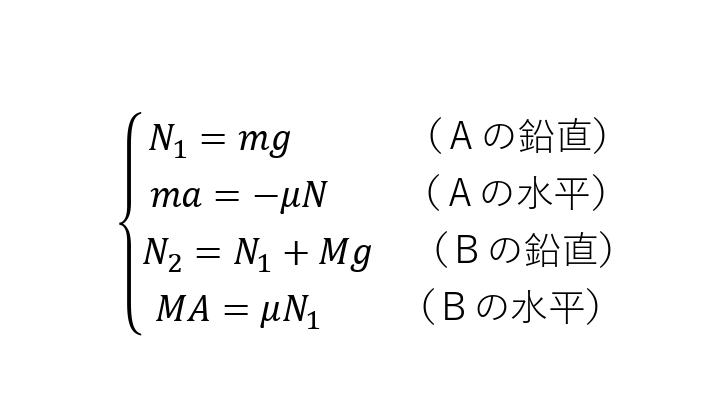
整理して
\(\normalsize{a}=-\normalsize{\mu}\normalsize{g}\)、\(\normalsize{A}=\frac{ m }{ M }\normalsize{\mu}\normalsize{g}\)
\(\normalsize{V}=\normalsize{at}+\normalsize{V}_{0}\) より[おまけを確認]
(\(\normalsize{A}\)の加速度)=\(\normalsize{at}+\normalsize{v}_{0}\)
(\(\normalsize{B}\)の加速度)=\(\normalsize{At}\)
\(\normalsize{A}\)が\(\normalsize{B}\)の上で止まるときは
\(\normalsize{A}\)の速度と\(\normalsize{B}\)の速度が一致しているときだから
(\(\normalsize{A}\)の速度)=(\(\normalsize{B}\)の速度)
\(\normalsize{at}+\normalsize{v}_{0}=\normalsize{At}\)
\(-\normalsize{\mu}\normalsize{gt}+\normalsize{v}_{0}=\frac{ m }{ M }\normalsize{\mu}\normalsize{gt}\)
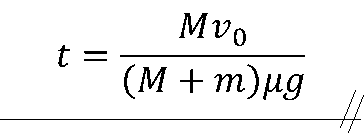
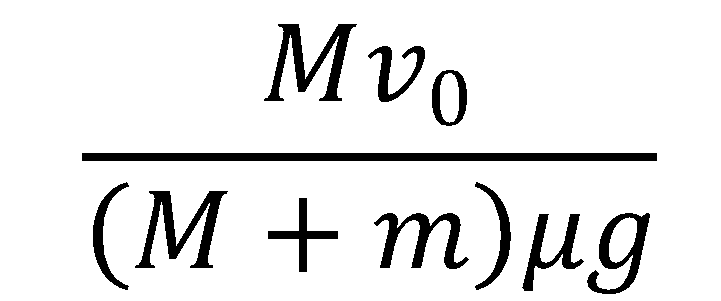
力学に限らず何かを理解するときは、まずは、大まかに全体を把握して細かいところを後で補強していくのが良いかと思います。
今回は、細かいワザ(摩擦が\(\normalsize{\mu}\normalsize{N}\)、右向きを正としたら左向きはマイナスで表す、など)もあったかと思いますが、全体の解く流れが明確になったと感じていただけたら嬉しいです。